范畴论完全装逼手册 / Grokking Monad
第三部分:搞基猫呢
第二部分介绍了一些实用的monad instances,这些 monad 都通过同样的抽象方式,解决了分离计算与副作用的工作。
通过它们可以解决大多数的基本问题,但是正对于复杂业务逻辑,我们可能还需要一些更高阶的 monad 或者 pattern。
当有了第一部分的理论基础和第二部分的实践,这部分要介绍的猫呢其实并不是很搞基。通过这一部分介绍的搞基猫呢, 我们还可以像 IO monad 一样,通过 free 或者 Eff 自定义自己的计算,和可能带副作用的解释器。
RWS
RWS 是缩写 Reader Writer State monad, 所以明显是三个monad的合体。如果已经忘记 Reader Writer 或者 State,请到第二部分复习一下。
一旦把三个 monad 合体,意味着可以在同一个 monad 使用三个 monad 的方法,比如,可以同时使用 Reader 的 ask, State 的 get, put, 和 Writer 的 tell
readWriteState = do
e <- ask
a <- get
let res = a + e
put res
tell [res]
return res
runRWS readWriteState 1 2
-- (3 3 [3])
注意到跟 Reader 和 State 一样,run的时候输入初始值
其中 1 为 Reader 的值,2 为 State 的初始状态.
Monad Transform
你会发现 RWS 一起用挺好的,能读能写能打 log,但是已经固定好搭配了,只能是 RWS ,如果我还想加入其它的 Monad,该怎么办呢?
这时候,简单的解决方案是加个 T,比如对于 Reader,我们有 ReaderT,RWS,也有对应的 RWST。其中 T 代表 Transform。
ReaderT
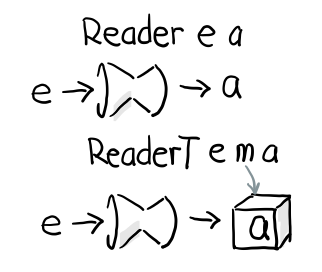
让我来通过简单的 ReaderT 来解释到底什么是 T 吧, 首先跟 Reader 一样我们有个 runReaderT
newtype ReaderT e m a = ReaderT { runReaderT :: e -> m a }
比较一下 Reader 的定义
newtype Reader e a = Reader { runReader :: (e -> a) }
有没有发现多了一个 m, 也就是说, runReader e 会返回 a, 但是 runReaderT e 则会返回 m a
instance (Monad m) => Monad (ReaderT e m) where
return = lift . return
r >>= k = ReaderT $ \ e -> do
a <- runReaderT r e
runReaderT (k a) e
再看看 monad 的实现, 也是一样的, 先 run 一下 r e 得到结果 a, 应用函数 k 到 a, 再 run 一把.
问题是, 这里的 return 里面的 lift 是哪来的?
instance MonadTrans (ReaderT e) where
lift m = ReaderT (const m)

这个函数 lift 被定义在 MonadTrans 的实例中, 简单的把 m 放到 ReaderT 结果中.
例如, lift (Just 1) 会得到 ReaderT, 其中 e 随意, m 为 Maybe Num
重点需要体会的是, Reader 可以越过 Maybe 直接操作到 Num, 完了再包回来.
有了 ReaderT, 搭配 Id Monad 就很容易创建出来 Reader Monad
type Reader r a= ReaderT r Identity a
越过 Id read 到 Id 内部, 完了再用 Id 包回来, 不就是 Reader 了么
ReaderT { runReaderT :: r -> Identity a }
-- Identity a is a
ReaderT { runReaderT :: r -> a }
Alternative
这个 typeclass 提供 <|> 函数, 表示要么计算左边, 要么计算右边
class Applicative f => Alternative f where
empty :: f a
(<|>) :: f a -> f a -> f a
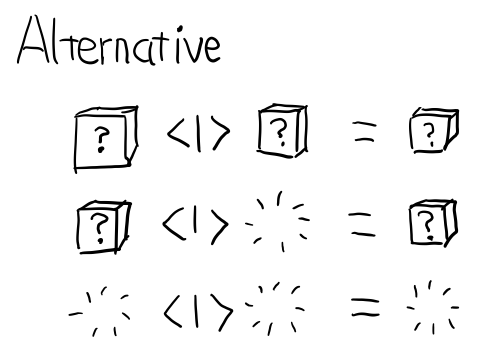
其实就是 Applicative 的 或
比如:
Just 1 <|> Just 2 -- Just 1
Just 1 <|> Nothing -- Just 1
Nothing <|> Just 1 -- Just 1
Nothing <|> Nothing -- Nothing
MonadPlus
这跟 Alternative 是一毛一样的, 只是限制的更细, 必须是 Monad才行
class (Alternative m, Monad m) => MonadPlus m where
mzero :: m a
mzero = empty
mplus :: m a -> m a -> m a
mplus = (<|>)
看, 实现中直接就调用了 Alternative 的 empty 和 <|>
ST Monad
ST Monad 跟 State Monad 的功能有些像, 不过更厉害的是, 他不是 immutable 的, 而是 "immutable" 的在原地做修改. 改完之后 runST 又然他回到了 immutable 的 Haskell 世界.
sumST :: Num a => [a] -> a
sumST xs = runST $ do -- do 后面的事情会是不错的内存操作, runST 可以把它拉会纯的世界
n <- newSTRef 0 -- 在内存中创建一块并指到 STRef
forM_ xs $ \x -> do -- 这跟命令式的for循环改写变量是一毛一样的
modifySTRef n (+x)
readSTRef n -- 返回改完之后的 n 的值
Free Monad
上一章说过的 RWS Monad 毕竟是固定搭配,当你的业务需要更多的 Monad 来表示 Effect 时, 我们就需要有那么个小猪手帮我们定义自己的 Monad。
那就是 Free, Free 可以将任意 datatype lift 成为 Monad
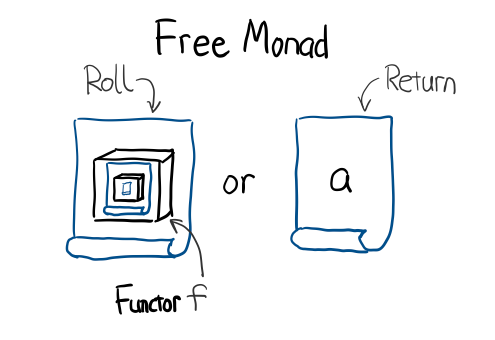
Free
先看 Free 什么定义:
data Free f a = Roll (f (Free f a)) | Return a
seal trait Free[F[_], A]
case class Roll[S[_], A](a: S[Free[S,A]]) extends Free[S, A]
case class Return[F[_], A](a: A) extends Free[S, A]
其中 f 就是你业务需要的 effect 类型, a 是这个 effect 所产生的返回值类型。
右边两种构造函数,如果把 Role 改成 Cons, Return 改成 Nil 的话, 是不是跟 List 其实是 同构 的呢? 所以如果想象成 List, 那么 f 在这里就相当于 List 中的一个元素.
到那时, >>= 的操作又跟 List 略有不同, 我们都知道 >>= 会把每一个元素 map 成 List, 然后 flatten, 但 Free 其实是用来构建
顺序的 effect 的, 所以:
instance Functor f => Monad (Free f) where
return a = Return a
Return a >>= fn = fn a
Roll ffa >>= fn = Roll $ fmap (>>= fn) ffa
implicit def monadForFree[S[_]](implicit F:Functor[S]): Monad[Free[S, ?]] =
new Monad[Free[S, ?]] {
def pure[A](a: A): Free[S, A] = Return(a)
def map[A, B](fa: Free[S, A])(f: A => B): Free[S, B] = fa.flatMap(a=>Return(f(a)))
def flatMap[A, B](a: Free[S, A])(f: A => Free[S, B]): Free[S, B] = a match {
case Return(a) => f(a)
case Roll(a) => Roll(F.map(a)(_.flatMap(f)))
}
}
你会发现 >>= 会递归的 fmap 到 Roll 上, 直到最后一个 Return.
比如, 如果你有一个 program 有三种副作用 Eff1, Eff2, Eff3
data Eff a = Eff1 a | Eff2 a | Eff3 a
program = do
a <- liftF $ Eff1 1
b <- liftF $ Eff2 2
c <- liftF $ Eff3 3
return a + b + c
sealed trait Eff[A] {
def eff1[A](a: A): Eff[A] = Free.liftF[Eff, A](Eff1(a))
def eff2[A](a: A): Eff[A] = Free.liftF[Eff, A](Eff2(a))
def eff3[A](a: A): Eff[A] = Free.liftF[Eff, A](Eff3(a))
}
case class Eff1[A](a: A) extends Eff[A]
case class Eff2[A](a: A) extends Eff[A]
case class Eff3[A](a: A) extends Eff[A]
val program = for {
a <- eff1(1)
b <- eff2(2)
c <- eff3(3)
} yield a + b + c
如果我们把 program 展开, 每一步 >>= 大概是这样:
liftF $ Eff1 1
展开既是:
Roll (Eff1 (Return 1))
代入到 program 即:
program = Roll (Eff1 (Return 1)) >>= \a -> do
b <- liftF $ Eff2 2
c <- liftF $ Eff3 3
return a + b + c
val program = Roll(Eff1(Return(1))).flatMap(a=>
for {
b <- eff2(2)
c <- eff3(3)
} yield a + b + c
)
用 Free 的 >>= 公式 Roll ffa >>= fn = Roll $ fmap (>>= fn) ffa 去展开上面就得到:
program = Roll $ Eff1 (Return 1 >>= fn1)) where
fn1 = \a -> do
b <- liftF $ Eff2 2
c <- liftF $ Eff3 3
return a + b + c
val fn1 = (a: Int) =>
for {
b <- eff2(2)
c <- eff3(3)
} yield a + b + c
val program = Roll(Eff1(Return(1).flatMap(fn1)))
Return 1 >>= fn1 我们都知道怎么展开:
program = Roll $ Eff1 (fn1 1) where
fn1 = \a -> do
b <- liftF $ Eff2 2
c <- liftF $ Eff3 3
return a + b + c
val fn1 = (a: Int) =>
for {
b <- eff2(2)
c <- eff3(3)
} yield a + b + c
val program = Roll(Eff1(fn1(1)))
展开 fn1
program = Roll $ Eff1 do
b <- liftF $ Eff2 2
c <- liftF $ Eff3 3
return 1 + b + c
val program = Roll(Eff1(for {
b <- eff2(2)
c <- eff3(3)
} yield 1 + b + c))
同样的步骤展开 Eff2
program = Roll $ Eff1 $ Roll $ Eff2 do
c <- liftF $ Eff3 3
return 1 + 2 + c
val program = Roll(Eff1(Roll(Eff2(for {
c <- eff3(3)
} yield 1 + 2 + c))))
和 Eff3
program = Roll $ Eff1 $ Roll $ Eff2 $ Roll $ Eff3 do
return 1 + 2 + 3
val program = Roll(Eff1(Roll(Eff2(Roll(Eff3(Return(1 + 2 + 3)))))))
最后的 program 是不是很像 List 的 Cons 和 Nil 呢?
program = Roll $ Eff1 $ Roll $ Eff2 $ Roll $ Eff3 $ Return 1 + 2 + 3
但是, 细心的你可能早都发现了 Eff 这货必须是个 Functor 才行. 那我们如何随便定义一个 data Eff 直接能生成 Functor Eff 的实例呢?
Coyoneda
希望你还依然记得第一部分的米田 共 引理
data CoYoneda f a = forall b. CoYoneda (b -> a) (f b)
trait CoYoneda[F[_], A] {
type P
val fi: F[P]
val ks: P => A
}
object CoYoneda{
type Aux[F[_], A, B] = CoYoneda[F, A] { type P = B }
def apply[F[_], A, B](f: B => A)(fa: F[B]): Aux[F, A, B] = new CoYoneda[F, A] {
type P = B
val fi = fa
val ks = f
}
}
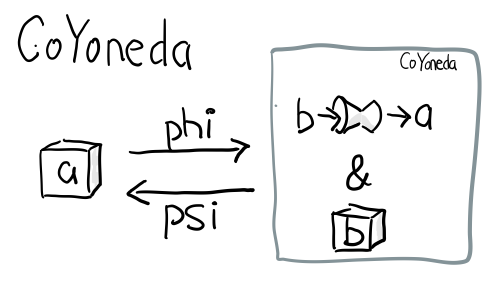
事实上很简单可以把任何 f 变成 CoYoneda f
phi :: f a -> CoYoneda f a
phi fa = CoYoneda id fa
def phi[F[_], A](fa: F[A]): Aux[F, A, A] = apply(identity)(fa)
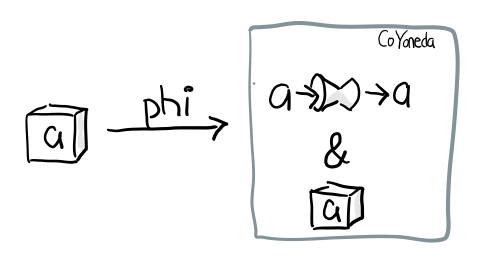
诀窍就是 id, 也就是你把 b 变成 a, 再把 fa 放到 CoYoneda 里就好了
当 f 是 Functor 时, 又可以把 CoYoneda 变成 f
psi :: Functor f => CoYoneda f a -> f a
psi (CoYoneda g fa) = fmap g fa
def psi[F[_]:Functor, A](fa: CoYoneda[F, A]): F[A] = Functor[F].map(fa.fi)(fa.ki)

反过来的这个不重要, 重要的是 phi, 因为如果你可以把任何 f 变成 CoYoneda f, 而 CoYoneda f 又是 Functor,
我们不就免费得到一个 Functor?
instance Functor (Coyoneda f) where
fmap f (Coyoneda g fb) = Coyoneda (f . g) fb
implicit def freeFunctorForCoyoneda[F[_]]: Functor[CoYoneda[F, _]] =
new Functor[CoYoneda[F, _]] {
def map[A, B, C](cfa: Aux[F, A, C])(f: A => B): Aux[F, B, C] = new CoYoneda[F, B] {
type P = C
val fi: F[C] = cfa.fi
val ki: C => B = f compose cfa.ki
}
}
Free Functor
比如我们的 Eff 就可以直接通过 phi 变成 CoYoneda Eff, 从而得到免费的 Functor
data Eff a = Eff1 a | Eff2 a | Eff3 a
program = Roll (phi (Eff1 (Roll (phi (Eff2 (Return Int))))))
val program = Roll(phi(Eff1(Roll((phi(Eff2(Roll(phi(Eff3(Return(1 + 2 + 3)))))))))))
Interpreter
构造完一个 free program 后,我们得到的是一个嵌套的数据结构, 当我们需要 run 这个 program 时, 我们需要 foldMap 一个 Interpreter 去一层层拨开 这个 free program.
foldMap :: Monad m => (forall x . f x -> m x) -> Free f a -> m a
foldMap _ (Return a) = return a
foldMap f (Roll a) = f a >>= foldMap f
def foldMap[F[_], M[_]: Monad, A](free: Free[F, A])(fk: F ~> M): M[A] = free match {
case Return(a) => Monad[M].pure(a)
case Roll(a) => fk(a).flatMap(foldMap(_)(fk))
}