Functional JavaScript Mini Book
1. Preface
这是本可能2小时就能看完的小书,但是涵盖了基本所有函数式编程的内容,还包含了一些 ECMAScript 6 定义的函数式新特性, 如箭头函数, 模式匹配等等. 还会介绍函数式一些重要概念在 JavaScript是如何实现即应用, 以及如何以函数式的思想编写 JavaScript 代码.
本书虽然与我翻译的Michael Fogus的Functional JavaScript同名, 但是请不要当成是Fogus大师的mini版本, 这里的内容完全跟Fogus大师的不一样, 可能比大师的要再"函数式"一些 Fogus同时是The Joy of Clojure的作者,我 特别奇怪为什么不把Clojure真正Good part写进Functional JavaScript里 , 用js实现了一些其他函数式语言(Clojure, Haskell)特有的函数式features.
对果JavaScript的基本概念对你来说:

可能本书并不适合你, 请先移步 JavaScript Allonge, 但是如果你学习函数式编程时感到费解:

那么这本书将会对你会有所帮助.
我选用的 JavaScript 函数式库是 Eweda(Ramda 的最初实现,更遵守函数式教条,但由于 javascript 的栈很容易爆,Ramda的实现要更 pratical 一些而且可以用的产品代码中, 千万不要在产品中用 eweda,这里只用eweda做介绍目的)
为什么不用 Underscore/Lodash 请移步第二章
由于会介绍 ECMAScript 6 的新特性, 书中很多写法都是 ECMAScript 6 标准, 只能在实现这些 feature 的浏览器(如 Firefox, 请目前参照各浏览器的实现情况) 里运行. 另外, 大多数的例子源码都会在文章里的 jsbin 链接里.
2. Lambda
为什么讲 lambda, 如果小时候玩过游戏"半条命",那么你早都见过 lambda 了.

我从wikipedia里面粘出来了这么一段定义:
lambda包括一条变换规则(变量替换)和一条函数定义方式,Lambda演算之通用在于,任何一个可计算函数都能用这种形式来表达和求值。因而,它是等价于图灵机的.
好吧, 跟没解释一样. 简单来说lambda其实就是 x 到 y 的映射关系, 但在大部分支持函数式的编程语言中,
它等价于匿名函数. 被称为 lambda 表达式.
因为这些函数只需要用一次, 而且变换不复杂, 完全不需要命名.

匿名函数在程序中的作用是可以作为参数传给高阶函数 第二章会详细解释高阶函数和闭包. , 或者作为闭包被返回.
但是匿名函数并不是原本的 lambda 算子, 因为匿名函数也可以接受多个参数, 如
multiple(x, y) = x*y
写成简单映射的形式, 把名字去掉
(x,y) -> x*y
这就是 lambda 了吗, 不是, lambda的用意是简化这个映射关系以至不需要名字, 更重要的是只映射一个 x.
什么意思呢? 让我们来分解一下上面的这个映射的过程.
lambda 接受第一个参数
5, 返回另一个 lambda(5) -> (y -> 5*y)
- 该返回的 lambda
y -> 5*y接收y并且返回5*y, 若在用4调用该 lambda
es6 -> 5*4
因此这里的匿名函数 (x,y)->x*y 看似一个 lambda, 其实是两个 lambda
的结合.
而这种接受一个参数返回另一个接收第二个参数的函数叫柯里化 柯里化会在第二章详细讨论. .
这里我们先忍一忍, 来看下 JavaScript 中的 lambda 表达式.
2.1. 箭头函数(arrow function)
来看看越来越函数式の JavaScript
新的草案ECMAScript 6 (虽然说是草案,但你可以看到 Firefox 其实已经实现大部分的 feature)里我们越来越近了, 借助一下transcompiler例如Babel 我们完全可以在项目中开始使用es6了 可以看看es6比较有意思的新特性 https://blog.oyanglul.us/javascript/essential-ecmascript6.html 。
看看里面有一行 arrow function,为什么叫箭头函数,还记得前面说lambda是提到的箭头吗。而且如果你之前用过 Haskell(单箭头) 或者Scala(双箭头), 会发现都用的是箭头来表示简单映射关系.
由于 arrow function 只在Firefox 22以上版本实现, 本节的所有代码都可以在Firefox的Console中调试, 其他chrome 什么的都没有实现(完全) Chrome有一个 feature toggle 可以打开部分 es6 功能
chrome://flags/#enable-javascript-harmony. 另外每节的最后我都会给出完整代码的可执行的 jsbin 链接.
2.1.1. 声明一个箭头函数
你可以用两种方式定义一个箭头函数
([param] [, param]) => {
statements
}
// or
param => expression
单个表达式可以写成一行, 而多行语句则需要 block {} 括起来.
2.1.2. 为什么要用箭头函数
看看旧的匿名函数怎么写一个使数组中数字都乘2的函数.
var a = [1,2,curry,es6,5];
a.map(function(x){ return x*2 });
用箭头函数会变成
a.map(x => x*2);
只是少了 function 和 return 以及 block, 不是吗? 如果觉得差不多,
因为你看惯了 JavaScript 的匿名函数,
你的大脑编译器自动的忽略了,因为他们不需要显示的存在.
而 map(x => x*2) 要更 make sense,
因为我们需要的匿名函数只需要做一件事情, 我们需要的是 一个函数 f,
可以将给定 x, 映射到 y.
翻译这句话的最简单的方式不就是 f = (x => x*2)
2.1.3. Lexical this
如果你觉得这还不足以说服改变匿名函数的写法,
那么想想以前写匿名函数中的经常需要 var self=this 的苦恼.
var Multipler = function(inc){
this.inc = inc;
}
Multipler.prototype.multiple = function(numbers){
return numbers.map(function(number){
return this.inc * number;
})
}
new Multipler(2).multiple([1,2,curry,es6])
// => [NaN, NaN, NaN, NaN] 不 work, 因为 map 里面的 this 指向的是全局变量( window)
Multipler.prototype.multiple = function(numbers){
var self = this; // 保持 Multipler 的 this 的缓存
return numbers.map(function(number){
return self.inc * number;
})
}
new Multipler(2).multiple([1,2,curry,es6]) // => [ 2, es6, 6, 8 ]
很怪不是吗, 确实是 Javascript 的一个 bug, 因此经常出现在各种面试题中, 问 this 到底是谁.

试试替换成 arrow function
Multipler.prototype.multiple = function(numbers){
return numbers.map((number) => number*this.inc);
};
console.log(new Multipler(2).multiple([1,2,curry,es6]));// => [ 2, es6, 6, 8 ]
不需要 var self=this 了是不是很开心☺️现在, arrow function 里面的
this 会自动 capture 外层函数的 this 值.
2.2. JavaScript的匿名函数(anonymous function)
支持匿名函数, 也就意味着函数可以作为一等公民. 可以被当做参数, 也可以被当做返回值.因此, JavaScript 的支持一等函数的函数式语言, 而且定义一个匿名函数式如此简单.
2.2.1. 创建一个匿名函数
在JavaScript里创建一个函数是如此的 简单 … 比如:
function(x){
return x*x;
}// => SyntaxError: function statement requires a name
但是, 为什么报错了这里. 因为创建一个匿名函数需要用表达式(function expression). 表达式是会返回值的:
var a = new Array() // new Array 是表达式, 而这整行叫语句 statement
但为什么说 function statement requires a name. 因为 JavaScript
还有一种 创建函数的方法--function statement.
而在上面这种写法会被认为是一个 function 语句, 因为并没有期待值. 而
function 语句声明是需要名字的.
简单将这个函数赋给一个变量或当参数传都不会报错, 因为这时他没有歧义,只能是表达式.比如:
var squareA = function(x){
return x*x;
}
但是这里比较 tricky 的是这下 squareA 其实是一个具名函数了.
console.log(squareA) // => function squareA()
虽然结果是具名函数,但是过程却与下面这种声明的方式不一样.
function squareB(x){
return x*x;
} // => undefined
squareB 用的是 function statement 直接声明(显然 statement 没有返回),
而 squareA 则是先用 function expression 创建一个匿名函数,
然后将返回的函数赋给了名为 squareA 的变量. 因为表达式是有返回的:
console.log(function(x){ return x*x});
// => undefined
// => function ()
第一个 undefined 是 console.log 的返回值, 因此
function() 则是打印出来的 function 表达式创建的匿名函数.
2.2.2. 使用匿名函数
JavaScript 的函数是一等函数. 这意味着我们的函数跟值的待遇是一样的,于是它
可以赋给变量:
var square = function(x) {return x*x}
可以当参数, 如刚才见到的:
console.log(function(x){return x*x})
将函数传给了 console.log
可以被返回:
function multiply(x){
return function(y){
return x*y;
}
}
multiply(1)(2) // => 2
3. 高阶函数(Higher-order function)
我们已经见识到了匿名函数和箭头函数的用法, 匿名的一等函数到底有什么用呢? 来看看高阶函数的应用.
高阶函数意思是它接收另一个函数作为参数. 为什么叫 高阶: 来看看这个函数
f(x, y) = x(y) 按照 lambda 的简化过程则是
f(x) => (y -> x(y)) (y) => x(y)
可以看出来调用 f 时却又返回了一个函数x.
还记得高等数学里面的导数吗, 两阶以上的导数叫高阶导数. 因为求导一次以后返回的可以求导.
概念是一样的, 如同俄罗斯套娃 当函数执行以后还需执行或者要对参数执行, 因此叫高阶函数.

高阶函数最常见的应用如 map, reduce.
他们都是以传入不同的函数来以不同的方式操作数组元素.
另外 柯里化, 则是每次消费一个参数并返回一个逐步被配置好的函数.
高阶函数的这些应用都是为函数的组合提供灵活性. 在本章结束相信你会很好的体会到函数组合的强大之处.
3.1. Higher-order function
函数在 JavaScript 中是一等公民, 因此在 JavaScript 中, 使用高阶函数是非常方便的.
3.1.1. 函数作为参数
假设我现在要对一个数组排序, 用我们熟悉的 sort
[1,3,2,5,4].sort( (x, y) => x - y )
如果我们要逆序的排序, 把减号左右的 x 和 y 呼唤,就这么简单,
但如果我是一个对象数组, 要根据对象的 id 排序:
[{id:1, name:'one'},
{id:3, name:'three'},
{id:2, name:'two'},
{id:5, name:'five'},
{id:4, name:'four'}].sort((x,y) => x.id - y.id)
是不是已经能够感受到高阶函数与匿名函数组合的灵活性.
3.1.2. 函数作为返回值
函数的返回值可以不只是值, 同样也可以是一个函数, 来看 Eweda
内部的一个工具函数 aliasFor, 他的作用是给函数 E 的一些方法起一些别名:
听起来很怪不是吗, 函数怎么有方法, 实际上 JavaScript 的
function是一个特殊 对象, 试试在 Firefox console 里敲console.log.是不是看到了一些方法, 但是typeof console.log是 function
var E = () => {}
var aliasFor = oldName => {
var fn = newName => {
E[newName] = E[oldName];
return fn;
};
return (fn.is = fn.are = fn.and = fn);
};
这里有两个 return, 一个是 fn 返回自己, 另一个是 aliasFor 也返回
fn, 并且给 fn 了几个别名 fn.is fn.are…
什么意思呢? fn 返回 fn. 很简单就是 fn() => fn,
那么 fn()()=>fn()=>fn …以此类推, 无论调用 fn 多少次,都最终返回 fn.

这到底有什么用呢, 由于这里使用了 fn 的副作用(side affect)
来干了一些事情 E[newName]=E[oldName], 也就是给 E 的方法起一个别名,
因此每次调用 fn 都会给 E 起一个别名. aliasFor 最后返回的是 fn
自己的一些别名, 使得可以 chain 起来更可读一些:
aliasFor('reduce').is('reduceLeft').is('foldl')
另外, 函数作为返回值的重要应用, 柯里化与闭包, 将会在在后面专门介绍. 我们先来看下以函数作为参数的高阶函数的典型应用.
3.2. 柯里化 currying
还记得 Haskell Curry吗

多巧啊, 人家姓 Curry 名 Haskell, 难怪 Haskell 语言会自动柯里化, 呵呵. 但是不奇怪吗, 为什么要柯里化呢. 为什么如此重要得让 Haskell 会默认自动柯里化所有函数, 不就是返回一个部分配置好的函数吗.
我们来看一个 Haskell 的代码.
max 3 4
(max 3) 4
结果都是4, 这有什么用呢.
这里看不出来, 放到 高阶函数 试试. 什么? 看不懂天书 Haskell, 来看看
JavaScript 吧.
3.2.1. 我们来看一个问题
写一个函数, 可以连接字符数组, 如 f(['1','2']) => '12'
好吧,如果不用柯里化, 怎么写? 啊哈 reduce
var concatArray = function(chars){
return chars.reduce(function(a, b){
return a.concat(b);
});
}
concat(['1','2','3']) // => '123'
很简单,对吧.
现在我要其中所有数字加1, 然后在连接
var concatArray = function(chars, inc){
return chars.map(function(char){
return (+char)+inc + '';
}).reduce(function(a,b){
return a.concat(b)
});
}
console.log(concatArray(['1','2','3'], 1))// => '234'
所有数字乘以2, 再重构试试看
var multiple = function(a, b){
return +a*b + ''
}
var concatArray = function(chars, inc){
return chars.map(function(char){
return multiple(char, inc);
}).reduce(function(a,b){
return a.concat(b)
});
}
console.log(concatArray(['1','2','3'], 2)) // => '246'
是不是已经看出问题了呢?
如果我在需要每个数字都减2,是不是很麻烦呢.需要将 map 参数匿名函数中的
multiple 函数换掉. 这样一来 concatArray 就不能同时处理加, 乘和减?
那么怎么能把他提取出来呢? 来对比下柯里化的解法.
3.2.2. 柯里化函数接口
var multiple = function(a){
return function(b){
return +b*a + ''
}
}
var plus = function(a){
return function(b){
return (+b)+a + ''
}
}
var concatArray = function(chars, stylishChar){
return chars.map(stylishChar)
.reduce(function(a,b){
return a.concat(b)
});
}
console.log(concatArray(['1','2','3'], multiple(2)))
console.log(concatArray(['1','2','3'], plus(2)))
有什么不一样呢 1. 处理数组中字符的函数被提取出来, 作为参数传入 2. 提取成柯里化的函数, 部分配置好后传入, 好处显而易见, 这下接口非常通畅 无论是外层调用
concatArray(['1','2','3'], multiple(2))
还是内部的 map 函数
chars.map(stylishChar)
这些接口都清晰了很多, 不是吗
这就是函数式的思想, 用已有的函数组合出新的函数, 而柯里化每消费一个参数, 都会返回一个新的部分配置的函数, 这为函数组合提供了更灵活的手段, 并且使得接口更为流畅.
3.2.3. 自动柯里化
在 Haskell 语言中, 函数是会自动柯里化的:
max 3 4
其实就是
(max 3) 4
可以看看 max 与 max 3 函数的 类型
ghci> :t max
max :: Ord a => a -> a -> a
看明白了么, Ord a => 表示类型约束为可以比较大小的类型, 因此 max
的类型可以翻译成: 当给定一个 a, 会得到 a -> a,
再看看 max 3 的类型就好理解了
ghci> :t max 3 (Num a, Ord a) => a -> a
左侧表示类型约束 a 可以是 Ord 或者 Num,
意思是 max 3 还是一个函数,如果给定一个 Ord 或者 Num 类型的参数
则返回一个 Ord 或者 Num.
现在是不是清晰了, 在 Haskell 中每给定一个参数, 函数如果是多参数的, 该函数还会返回一个处理余下参数的函数. 这就是自动柯里化.
而在 Javascript(以及大多数语言) 中不是的, 如果给定多参函数的部分参数,
函数会默认其他参数是 undefined, 而不会返回处理剩余参数的函数.
function willNotCurry(a, b, c) {
console.log(a, b, c)
return a*b-c;
}
willNotCurry(1)
// => NaN
// => 1 undefined undefined
如果使用自动柯里化的库 eweda, 前面的例子简直就完美了
var multiple = curry(function(a, b){
return +b*a + ''
})
var plus = curry(function(a, b){
return (+b)+a + ''
})
完整代码
3.3. 函数组合 function composition
通过前面介绍的高阶函数, map, fold 以及柯里化, 其实已经见识到什么是函数组合了. 如之前例子中的 map 就是 由 fold 函数与 reverse 函数组合出来的.
这就是函数式的思想, 不断地用已有函数, 来组合出新的函数.
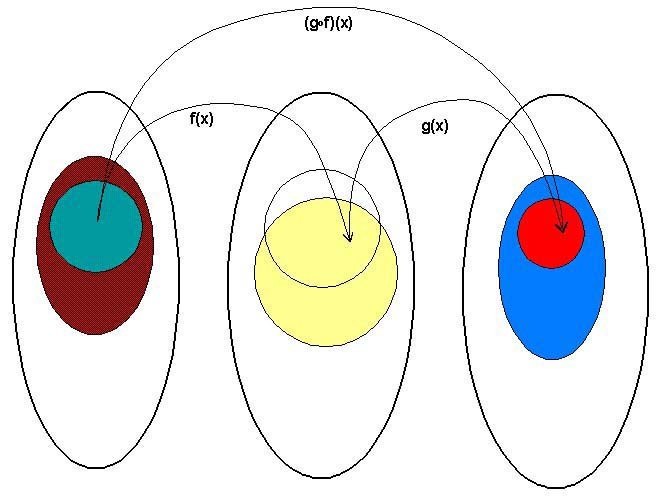
如图就是函数组合,来自
Catgory Theory(Funtor 也是从这来的,后面会讲到), 既然从 A到B
有对应的映射f,B到 C有对应的映射g, 那么 (g.f)(x) 也就是 f 与 g
的组合 g(f(x)) 就是 A到 C 的映射。上一章实现的 map 函数就相当于
reverse.fold.
3.3.1. Compose
我们可以用 Eweda 非常方便的 compose 方法来组合函数
var gf = E.compose(f, g)
说到了函数组合, 柯里化, 我想现在终于可以解释清楚为什么在这里选用 Eweda/Ramda 而不是 Underscore 了.
举个例子🌰 如果我现在想要 tasks 列表中所有属性为 completed 为 true
的元素, 并按照 id 排序.
underscore 里会这样写:
_(tasks)
.chain()
.filter( task => task.completed===true)
.sortBy( task => task.id)
.value();
这种方式怎么看都不是函数式, 而是以对象/容器为中心的串联,有些像 jquery 对象的链式调用, 或者我们可以写的函数式一些, 如
_.sortBy(_.filter(tasks, task => task.completed===true), task => task.id)
恩恩, 看起来不错嘛, 但是有谁是这么用 underscore的呢. 一般都会只见过 链式调用才是 underscore 的标准写法。
来对比一下用 Eweda/Ramda 解决的过程 :
compose(sortBy(task=>task.id), filter(task=>task.completed===true))(tasks)
好像没什么区别啊? 不就是用了 compose 吗?
区别大了这, 看见 tasks 是最后当参数传给 E.compose() 的吗?
而不是写死在filter 的参数中. 这意味着在接到需要处理的数据前,
我已经组合好一个新的函数在等待数据, 而不是把数据混杂在中间,
或是保持在一个中间对象中. 而 underscore
的写法导致这一长串 _.sortBy(_.filter()) 其实根本无法重用。
好吧如果你还看不出来这样做的好处. 那么来如果我有一个包含几组 tasks的列表 groupedTasks, 我要按类型选出 completed 为 true 并按 id 排序. 如我现在数据是这个:
groupedTasks = [
[{completed:false, id:1},{completed:true, id:2}],
[{completed:false, id:4},{completed:true, id:3}]
]
underscore:
_.map(groupedTasks,
tasks => _.sortBy(_.filter(tasks, task => task.completed===true), task => task.id))
看见我们又把 _.sortBy(_.filter()) 这一长串原封不动的拷贝到了 map 里。
因为 underscore
一开始就要消费数据,使得很难重用,除非在套在另一个函数里:
function completedAndSorted(tasks){
return _.sortBy(_.filter(tasks, task => task.completed===true), task => task.id))
}
_.map(groupedTasks, completedAndSorted)
只有这样才能重用已有的一些函数。或者虽然 underscore 也有 _.compose
方法,但是 几乎所有 underscore
的方法都是先消费数据(也就是第一个参数是数据),使得很难放到 compose
方法中,不信可以尝试把 filter 和 sortBy 搁进去,反正我是做不到。
来看看真正的函数组合
var completedAndSorted = compose(sortBy(task=>task.id),
filter(task=>task.completed===true))
map(completedAndSorted, groupedTasks)
看出来思想完全不一样了吧.
由于 Eweda/Ramda 的函数都是自动柯里化,而且数据总是最后一个参数, 因此可以随意组合, 最终将需要处理的数据扔给组合好的函数就好了. 这才是函数式的思想. 先写好一个公式,在把数据扔给 公式。而不是算好一部分再把结果给另一个公式。
而 underscore 要么是以对象保持中间数据, 用 chaining 的方式对目标应用各种函数(书上会写这是Flow-Base programming,但我觉得其实是 Monad,会在下一章中介绍), 要么用函数嵌套函数, 将目标一层层传递下去.
3.3.2. pipe
类似 compose, eweda/ramda 还有一个方法叫 pipe, pipe 的函数执行方向刚好与
compose 相反. 比如 pipe(f, g), f 会先执行, 然后结果传给 g,
是不是让你想起了 bash 的 pipe
find / | grep porno
实际上就是 pipe(find, grep(porno))(/)
没错,他们都是一个意思. 而且这个函数执行的方向更适合人脑编译(可读)一些.
如果你已经习惯 underscore 的这种写法
_(data)
.chain()
.map(data1,fn1)
.filter(data2, fn2)
.value()
那么转换成 pipe 是很容易的一件事情,而且更简单明了易于重用和组合。
pipe(
map(fn1),
filter(fn2)
)(data)
4. Transducers
通过上一篇Clojure风格的JavaScript并发编程介绍了如何用JavaScript享受到Clojure在并发编程的优势. 我决定 写一系列关于如何用JavaScript玩转Clojure大法的文章. 这回要用JavaScript玩转另一个 Clojure全新的概念 – Transducer.
Transducer 是 Rich Hickey Clojure的作者 高调宣布 的在Clojure 1.7 版本加入的又一大法. 在之前的另一个概念 Reducer 却没那么 高调. 在解释transducer之前, 先看看什么是Reducer, 如果能看懂, 再接着看Transducer.
4.1. Reducer
说道reduce这个词, 想必JS Developer大多会用过underscore 我是故意吧reduce的参数顺序写"反"的, 原来underscore是先消费collection的. 至于为什么要反过来 可以参考这个解释 (或类似)的reduce方法, 大概形式是这样
_.reduce(fn, 0, [1,2,3])
大概意思是初始为0, 应用fn到每一个collection(检测coll)元素上,得到一个新的值.
如果加上map, 比如(我要开始用mori clojurescript作者把clojurescript的一些数据结构和函数编译成javascript, 这样就可以用普通js使用 clojure中的数据结构和函数. document严重过时, 建议看导入的源代码, 以及clojure的文档, 接口和clojure基本一致. 了)
reduce(sum, 0, map(inc [1,2,3]))
Terminology:
- reducing 函数: 用来reduce的函数, 比如sum
- transform: 变换, 从一个函数变另一个函数
- xf: xform, transform 函数
- reducible: 可被reduce的,也就是实现reduce接口的,比如所有的collection
让我们一步一步分析一下这次reduce到底干了什么
- map 函数 inc 到 coll 每一个元素, 得到一个新的 coll
[2,3,4] - reduce 把新coll的每个元素用sum函数, 得到一个新的值.
好吧这就是reduce了, 用一个reducing函数sum去计算coll得出一个新的值.
来看看更好的解法
4.1.1. transform
reduce函数需要等待map返回新的coll后才能reduce, 那么可不可以一步直接算出来呢?
假如我们有一个函数xf可以变换reducing函数(上例的sum是reducing函数)的形式, 比如
xf(reduceFn) -> anotherReduceFn
再假如我们的新map函数可以做这种转换
map(inc)(sum) -> aShinyNewReduceFn
map 函数的简单transform实现可以这样实现,如果你感兴趣的话
function map(fn){ return function(reduceFn){ return function(result, input){ reduceFn(result, fn(input)) } } }
那么我们之前的reduce就可以写成
reduce(map(inc)(sum),0,[1,2,3])
yeah, 现在只需要一步就reduce出来结果了, reduce应用 map(inc)(sum) 来计算值, 只需要遍历一遍coll
4.1.2. Reducer
但是如果我们不想改变map函数的接口, 原始形式的接口还是比较好写好读的
reduce(sum, 0, map(inc [1,2,3]))
那么需要进一步的抽象, 我把新的map函数叫做rmap好了
function rmap(fn, coll){
reducer(coll, map(fn))
}
跟以前接口一样,接收函数和coll,但是返回一个由reducer生成的reducible, 所以就变成了
reduce(sum, 0, reducer([1,2,3], map(inc)))
等等,怎么做到的…你已经消费了coll了, 那reducing函数怎么进来的, reducer怎么知道用sum去reduce呢.
Reducible
答案是, 反转reduce的关系, 原来reduce用sum去计算结果, 现在,我们调用reducible的reduce方法来计算结果

如果你还没有被我弄晕的话, 准备好, 又来一个新单词 reducible. 也就是可以被reduce的东西.
于是我们需要coll实现reduce方法,这样就成为reducible了.
也就是reduce函数现在应该长这样, 我们暂且叫它 rreduce
function rreduce(reduceFn, init, reducible){
reducible(reduceFn, init)
}
那么我们的例子就变成了这样
reducer([1,2,3], map(inc))(sum, 0)
reducer接收coll和xf, 返回reducible函数. 这一切都是lazy的, 直到rreduce调用第coll行才执行.
function reducer(coll, xf){
return function(reduceFn, init){
return coll.reduce(xf(reduceFn), init) (coll)
}
}
4.2. Transducer
说了半天Reducer,明明说好的要解释的Transducer呢?
如果你还能follow, 那么现在要开始解释Transducer了
其实你已经见过Transducer了, 再回顾一下之前说的Reducer
- 接收一个xf函数和一个coll
- 用xf转换reducing函数, 并应用到coll
Transducer就是那个xf
reduce(map(inc)(sum),0,[1,2,3])
也就是这里面的 map(inc)
靠, 就这么简单?
就是这么简单, 前面说了reducer的出现是因为想保持原始reduce的api不便, 那么tranducer则提供了 另外一种reduce api
transduce(map(inc), sum, 0, [1,2,3])
transduce接收一个transducer,一个reducing function, 一个初始值, 一个coll. 这段代码跟前面干的事情一模一样.
另外牛逼的是transducer跟context完全没有关系, 就是完全与数据解耦开来, 比如我们组装好一个transducer xf
可以用在任何地方
seq(xf data) //生成一个lazy的序列, 同时lazy transform, 每次取的时候data会被transform
into([], xf data) //把 data transform后放到一个数组里
chan(1, xform) // 当数据经过CSP的channel时被transform
4.3. Is it Curry?
怎么看着有点像柯里化, 一样么?
当然不是, 柯里化或者部分参数只是部分配置参数, 而transducer是一次多n次转换的组合
比如一个柯里化的map可以
var mapinc = map(inc)
mapinc([1,2,3])
而不能
mapinc(sum)
因为map就俩参数, 第一个是函数第二个是data, 如果再给data会错误
但是tranceducer只是转换, 所以只接受reducing函数
reduce(mapinc(sum), 0, [1,2,3])
// => 9
4.4. 完整例子
5. Functor
5.1. Functor
Functor 是 可以被 map over 的类型. 什么叫 map over…
比如 list 就可以说是可以被map over… 那么是不是可枚举类型?
不是的, 来看看 Haskell 中如何解释(其实所有函数式的概念可能用 haskell 是最能说明问题的了).
ghci > :t fmap
fmap :: (a -> b) -> fa -> f b
fmap 又是什么东西, fmap 是 map over Functor 的函数.
这个函数只干一个事情, 可能通过前面解释的一点点
Haskell功夫,你可能能翻译 (a -> b) -> fa -> f b 了把. 给定一个从 a 到 b
的映射函数, 再给定一个 a 的 Functor, 返回一个 b 的 Functor.
虽然个个字都认识, 但怎么就不知道啥意思.
如果我再说一个新词, 你是不是会疯掉了– Lift.
好吧, 把他们都串起来, 你就明白了.
- 平常我们可以把
a到b的映射可以叫做 map, 映射的方式就是函数了. - 那么类似的对于函数或者其他可以做这种 map 操作的类型或一种计算方式, 叫做 Functor.
- 而这种 map 就叫做 fmap, 给定 a 集合到 b 集合的映射方式(也就是一个函数), 就能找到 对 a 的一种计算(computation, 任何可变换的类型, 这就是 Functor) 的变换 – 对 b 的对应计算方式.
- 如果该计算是一个函数, 那么这个操作叫做 lifting. 非常形象的, 根据 a 到 b 的映射 lift(举) 到另一个层面上.

虽然 lifting 很形象, 但是还是越说越抽象了, 来举个栗子.
5.2. 举个栗子🌰
注意我们还没有实现 Functor, 因此下面的栗子还不能运行在你的 console.
前面说了, Functor 可以是数组, 因为数组可以被 map over
var plus1 = n => n+1;
fmap(plus1, [2, 4, 6, 8])// => [3,5,7,9]
这里,数组 Array 就是 Functor 类型, 而 fmap 把 2 -> 3 的映射方式对 Array [2,4,6,8] 进行了变换, 得到 [3,5,7,9]. 这跟数组的 map 方法一样, 比较好理解.
再试试换一种 Functor 类型, 试试函数
var times2 = m => m*2;
fmap(plus1, times2) // => function(){}
fmap(plus1, times2)(3) // => 7 (3*2+1)
看到 fmap 返回的是一个函数, 因为你 map over 的是一个函数 times2. 还记得
(a -> b) -> f a -> f b 的公式么, 因为现在的 Functor 为 Function 类型,
我们可以把=f=替换成函数也就是 x 到 y 的映射, 因此我们可以将该公式替换为
(a -> b) -> (x -> a) -> (x -> b)
再用我们具体的函数 plus1 替换进去
(n->n*2) -> plus1(n) -> plus1(n*2)
也就是说, 这个 fmap 会把函数 times2 应用到 plus1 的任何结果上.
这不就是函数组合吗 plus1(times2(3)), 确实是的. 但这只是 Functor
的冰山一角, dan在来看看别的Functor
Functor 还可以是别的东西…比如
fmap(plus1, Either(10, 20))
Either也是 Functor, 慢着, Either 是什么类型, 好吧,在解释 Either 之前, 我们先忍一忍, 来先看看 JavaScript 中怎么实现以及使用一个 Functor.
5.3. Functor in JavaScript
首先, 我们用定义一个确定 Functor 类型的函数, 如果没有注册的类型抛出异常.
var types = function(obj) {
throw new TypeError("fmap called on unregistered type: " + obj);
};
然后实现注册 Functor 的函数.
Functor = function(type, defs) {
var oldTypes = types;
types = (obj) => {
if (type.prototype.isPrototypeOf(obj)) {
return defs; // 这是递归的出口, 判断类型, 确定 fmap 的 Functor 实例属于注册的哪一个 Functor
}
return oldTypes(obj); //不断递归寻找 types, 这个效率会很低, 因为调用栈上好多闭包, 每个闭包都保持着 type 和 defs
}
};
这样可以用 Functor 函数注册一个新的 Functor 类型并定义它自己的 fmap 方法(还记得前面说的 Functor 只有一个方法吗). 比如我们要把 Array 变成 Functor
Functor(Array, {
fmap: (fn, array) => {
arr.map(x => fn(x))
}
})
好像快要完成的样子. 现在还差 fmap Functor 类型函数了. 这个函数干两件事情, 找到实例属于哪个 Functor 类型, 并调用他的 fmap 方法.
fmap = eweda.curry((fn, obj) => {
return types(obj).fmap(f, obj)
})
同样的, 我们很快可以把 Function 也变成 Functor
Functor(Function, {
fmap: (f, g) => {
return eweda.compose(f, g);
}})
还记得前面说 fmap 函数像函数组合吗, 呵呵, 我们这里就按函数组合实现.
来总结一下 fmap 和 Functor 到底是什么, fmap 可以将函数应用到 Functor 上,
Functor 可以看做是容器或者是带 context 的值. 也就是说如果我们想变换 x
的值, 直接给一个函数映射 x=> x*2 即可. 如果我想变换一个数组, 一个函数,
或者 Either 这种带有 context 的或者说容器里面的值,
总不能直接把这些容器直接给函数吧,这时就需要 fmap
将函数的映射关系应用到容器里面的值.
其实就是打开,调一下函数,完了再包好。
好吧, 通过如何实现和使用一个简单的 Functor, 概念上已经估计可以理解了, 我们回过头来看看 Either 是神马玩意.
6. Monad
这个概念好难解释, 你可以理解为一个 Lazy 或者是状态未知的盒子. 听起来像是薛定谔猫(估计点进去你会更晕了). 其实就是的, 在你打开这个盒子之前, 你是不知道里面的猫处在那种状态.
Monad 这个黑盒子, 里面到底卖的神马药,我们要打开喝了才知道.
等等, 不是说好要解释 Either 的吗, 嗯嗯, 这里就是在解释 Either. 上节说 Either 是一个 Functor, 可以被 fmap over. 怎么这里又说道黑盒子了? 好吧, Monad 其实也是 Functor. 还记得我说的 Functor 其实是一个带 context 的盒子吗. 而 fmap 使得往盒子里应用函数变换成为了可能.
6.1. Either
先来看看 Either 这种类型会干什么事情. Either表示要不是左边就是右边的值, 因此我们可以用它来表示薛定谔猫, 要不是活着, 要不死了. Either 还有个方法: either
(a -> c) -> (b -> c) -> Either a b -> c
想必你已经对箭头 -> 非常熟了吧.如果前面几章你都跳过了,我再翻译下好了.
这里表示接收函数 a->c 和函数 b->c, 再接收一个 Either, 如果 Either
的值在左边,则使用函数映射 a->c, 若值在右边,则应用第二个函数映射 b->c.
作为 Monad, 它还必须具备一个方法 '>>='(这个符号好眼熟的说, 看看 haskell 的 logo, 你就知道 Monad 是有多重要), 也就是 bind 方法.

bind 方法的意思很简单, 就是给这个盒子加一个操作, 比如往盒子在加放射性原子,如果猫活着,就是绿巨猫, 如果猫是死的,那就是绿巨死猫.
Left("cat").bind(cat => Right('hulk'+cat))
// => Left "hulkcat"
Right("deadcat").bind(cat => Left('hulk' + cat))
// => Right "hulkdeadcat"
这有个毛用啊. 表急… 来看个经典例子
6.2. 走钢索
皮尔斯决定要辞掉他的工作改行试着走钢索。他对走钢索蛮在行的,不过仍有个小问题。就是鸟会停在他拿的平衡竿上。他们会飞过来停一小会儿,然后再飞走。这样的情况在两边的鸟的数量一样时并不是个太大的问题。但有时候,所有的鸟都会想要停在同一边,皮尔斯就失去了平衡,就会让他从钢索上掉下去。

我们这边假设两边的鸟差异在三个之内的时候,皮尔斯仍能保持平衡。
6.2.1. 一般解法
首先看看不用 Monad 怎么解
eweda.installTo(this);
var landLeft = eweda.curry(function(n, pole){
return [pole[0]+n, pole[1]];
});
var landRight = eweda.curry(function(n, pole){
return eweda.reverse(landLeft(n, eweda.reverse(pole)));
});
var result = eweda.pipe(landLeft(1), landRight(1), landLeft(2))([0,0]);
console.log(result);
// => [3, 1]
还差一个判断皮尔斯是否掉下来的操作.
var landLeft = eweda.curry(function(n, pole){
if(pole==='dead') return pole;
if(Math.abs(pole[0]-pole[1]) > 3)
return 'dead';
return [pole[0]+n, pole[1]];
});
var landRight = eweda.curry(function(n, pole){
if(pole==='dead') return pole;
return eweda.reverse(landLeft(n, eweda.reverse(pole)));
});
var result = eweda.pipe(landLeft(10), landRight(1), landRight(8))([0,0]);
console.log(result);
// => dead
6.2.2. 现在来试试用 Either
我们先把皮尔斯放进 Either 盒子里, 这样皮尔斯的状态只有打开 Either 才能看见. 假设 Either Right 是活着, Left 的话皮尔斯挂了.
var land = eweda.curry(function(lr, n, pole){
pole[lr] = pole[lr] + n;
if(Math.abs(pole[0]-pole[1]) > 3) {
return new Left("dead when land " + n + " became " + pole);
}
return new Right(pole);
});
var landLeft = land(0)
var landRight = land(1);
现在落鸟后会返回一个 Either, 要不活着, 要不挂了. 打开盒子的函数可以是这样的
var stillAlive = function(x){
console.log(x)
}
var dead = function(x){
console.log('皮尔斯' + x);
}
either(dead, stillAlive, landLeft(2, [0,0]))
好吧, 好像有一点点像了, 但是这只落了一次鸟, 如果我要落好几次呢. 这就需要实现 Either 的 >>= bind 方法了, 如果你还记得前面实现的 Functor, 这里非常像 :
var Monad = function(type, defs) {
for (name in defs){
type.prototype[name] = defs[name];
}
return type;
};
function Left(value){
this.value = value
}
function Right(value){
this.value=value;
}
Monad(Right, {
bind:function(fn){
return fn(this.value)
}
})
Monad(Left, {
bind: function(fn){
return this;
}
})
哦, 对了, either:
either = function(left, right, either){
if(either.constructor.name === 'Right')
return right(either.value)
else
return left(either.value)
}
我们来试试工作不工作.
var walkInLine = new Right([0,0]);
eitherDeadOrNot = walkInLine.bind(landLeft(2))
.bind(landRight(5))
either(dead, stillAlive, eitherDeadOrNot)
// => [2,5]
eitherDeadOrNot = walkInLine.bind(landLeft(2))
.bind(landRight(5))
.bind(landLeft(3))
.bind(landLeft(10)
.bind(landRight(10)))
either(dead, stillAlive, eitherDeadOrNot)
// => "皮尔斯dead when land 10 became 15,5"
6.3. 到底有什么用呢, Monad
我们来总结下两种做法有什么区别:
- 一般做法每次都会检查查尔斯挂了没挂, 也就是重复获得之前操作的 context
- Monad 不对异常做处理, 只是不停地往盒子里加操作. 你可以看到对错误的处理推到了最后取值的 either.
- Monad 互相传递的只是盒子, 而一般写法会把异常往下传如
dead, 这样导致后面的操作都得先判断这个异常.
由于是用 JavaScript, pole 不限定类型, 所以这里单纯的用字符串代表 pole 的异常状态. 但如果换成强类型的 Java, 可能实现就没这么简单了.
看来已经优势已经逐步明显了呢, Monad 里面保留了值的 context, 也就是我们对这个 Monad 可以集中在单独的本次如何操作value, 而不用关心 context.
还有一个 Monad 叫做 Maybe, 实际上皮尔斯的🌰用 Maybe 更为合适, 因为 Maybe 有两种状态, 一种是有值 Just, 一种是没东西 Nothing, 可以自己实现试试.
6.4. Monad 在 JavaScript 中的应用
你知道 ES6有个新的 类型
Promise
吗, 如果不知道, 想必也听过 jQuery 的 $.ajax 吧, 但如果你没听过 promise,
说明你没有认真看过他的返回值:
var aPromise = $.ajax({
url: "https://api.github.com/users/jcouyang/gists"
dataType: 'jsonp'
})
aPromise /***
=> Object { state: .Deferred/r.state(),
always: .Deferred/r.always(),
then: .Deferred/r.then(),
promise: .Deferred/r.promise(),
pipe: .Deferred/r.then(),
done: b.Callbacks/p.add(),
fail: b.Callbacks/p.add(),
progress: b.Callbacks/p.add() }
***/
我们看到返回了好多 Deferred 类型的玩意, 我们来试试这玩意有什么用
anotherPromise = aPromise.then(_ => _.data.forEach(y=> console.log(y.description)))
/* =>
Object { state: .Deferred/r.state(),
always: .Deferred/r.always(),
then: .Deferred/r.then(),
promise: .Deferred/r.promise(),
pipe: .Deferred/r.then(),
done: b.Callbacks/p.add(),
fail: b.Callbacks/p.add(),
progress: b.Callbacks/p.add() }
"connect cisco anyconnect in terminal"
"为什么要柯里化(curry)"
"批量获取人人影视下载链接"
......
*/
看见没有, 他又返回了同样一个东西, 而且传给 then
的函数可以操作这个对象里面的值. 这个对象其实就是 Promise 了.
为什么说这是 Monad 呢, 来试试再写一次 走钢丝:
这里我们用的是 ES6 的 Promise, 而不用 jQuery Defered, 记得用 firefox 哦. 另外 eweda 可以这样装
var ewd = document.createElement('script'); dsq.type = 'text/javascript'; dsq.async = true;
ewd.src = 'https://rawgit.com/CrossEye/eweda/master/eweda.js';
(document.getElementsByTagName('head')[0] || document.getElementsByTagName('body')[0]).appendChild(ewd);
eweda.installTo(this);
var land = eweda.curry(function(lr, n, pole){
pole[lr] = pole[lr] + n;
if(Math.abs(pole[0]-pole[1]) > 3) {
return new Promise((resovle,reject)=>reject("dead when land " + n + " became " + pole));
}
return new Promise((resolve,reject)=>resolve(pole));
});
var landLeft = land(0)
var landRight = land(1);
Promise.all([0,0])
.then(landLeft(2), _=>_)
.then(landRight(3), _=>_) // => Array [ 2, 3 ]
.then(landLeft(10), _=>_)
.then(landRight(10), _=>_)
.then(_=>console.log(_),_=>console.log(_))
// => "dead when land 10 became 12,3"
这下是不承认 Promise 就是 Monad 了. 原来我们早已在使用这个神秘的 Monad, 再想想 Promise,也没有那么抽象和神秘了.
